#include <stdio.h>
#include <stdlib.h>
void matrix_mul(int** matrix_A, int** matrix_B, int** matrix_C, int len, int i, int j, int k)
{
/* 행렬의 길이가 2일때 행렬곱 계산하고 종료하기 */
if (len == 2)
{
matrix_C[i][k] += matrix_A[i][j]* matrix_B[j][k] + matrix_A[i][j + 1]* matrix_B[j + 1][k];
matrix_C[i][k + 1] += matrix_A[i][j]* matrix_B[j][k + 1] + matrix_A[i][j + 1]* matrix_B[j + 1][k + 1];
matrix_C[i + 1][k] += matrix_A[i + 1][j]* matrix_B[j][k] + matrix_A[i + 1][j + 1]* matrix_B[j + 1][k];
matrix_C[i + 1][k + 1] += matrix_A[i + 1][j]* matrix_B[j][k + 1] + matrix_A[i + 1][j + 1]* matrix_B[j + 1][k + 1];
return;
}
/* 행렬의 길이가 2를 초과할때 재귀적 호출하기*/
else
{
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i, j, k);
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i, j + len/2, k);
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i, j, k + len/2);
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i, j + len/2, k + len/2);
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i + len/2, j, k);
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i + len/2, j + len/2, k);
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i + len/2, j, k + len/2);
matrix_mul(matrix_A, matrix_B, matrix_C, len/2, i + len/2, j + len/2, k + len/2);
}
}
int main() {
int size = 0, i = 0, j = 0, k = 0;
printf("입력할 행렬의 행과 열의 수를 입력하세요(2의 n승인 수로):");
scanf("%d", &size);
/* 계산할 두개의 행렬 동적 할당 해주기 */
int** matrix_A = (int**)malloc(sizeof(int) * size);
for (i = 0; i < size; i++) {
matrix_A[i] = (int*)malloc(sizeof(int) * size);
}
int** matrix_B = (int**)malloc(sizeof(int) * size);
for (i = 0; i < size; i++) {
matrix_B[i] = (int*)malloc(sizeof(int) * size);
}
int** matrix_C = (int**)malloc(sizeof(int) * size);
for (i = 0; i < size; i++) {
matrix_C[i] = (int*)malloc(sizeof(int) * size);
}
/* 행렬 입력받기 */
printf("첫번째 행렬을 입력하세요\n");
for (i = 0; i < size; i++) {
printf("%d번째 행:", i + 1);
for (j = 0; j < size; j++) {
scanf("%d", &matrix_A[i][j]);
}
fflush(stdin);
}
printf("두번째 행렬을 입력하세요\n");
for (i = 0; i < size; i++) {
printf("%d번째 행:", i + 1);
for (j = 0; j < size; j++) {
scanf("%d", &matrix_B[i][j]);
}
fflush(stdin);
}
/* 행렬 초기화시켜 주기*/
for (i = 0; i < size; i++) {
for (j = 0; j < size; j++) {
matrix_C[i][j] = 0;
}
}
matrix_mul(matrix_A, matrix_B, matrix_C, size, 0, 0, 0);//재귀함수 호출
/* 결과 값 출력해주기 */
for (i = 0; i < size; i++) {
for (j = 0; j < size; j++) {
printf("%d ", matrix_C[i][j]);
}
printf("\n");
}
free(matrix_A);
free(matrix_B);
free(matrix_C);
}시간 복잡도 계산
n의 길이를 가지는 행렬을 내적할 때의 시간복잡도를 T(n)이라고 하면 T(n) = T(divide) + T(conquer) + T(merge)로 나타낼 수 있다.
T(divide) = 1이고, n/2의 길이를 가지는 행렬의 곱을 8번 수행해야하기 때문에 T(conquer) =8T(n/2),
n x n 크기의 행렬의 각각의 원소에 대한 덧셈을 수행해야 함으로 T(merge) = n^2이다.
따라서

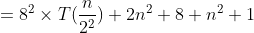

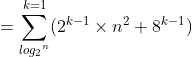
등비수열의 합 공식에 의해서 위 식의 합은

이고,
시간복잡도는
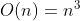
이다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [파이썬 알고리즘] 24. 이진 트리 합의 범위 (0) | 2022.05.06 |
|---|---|
| [파이썬 알고리즘] 23. 이진 탐색 트리(BST)를 더 큰 수 합계 트리로 (0) | 2022.05.05 |
| [파이썬 알고리즘 인터뷰] 22. 배열의 이진 탐색 트리 변환 (0) | 2022.05.03 |
| [파이썬 알고리즘] 21. 균형 이진 트리 (0) | 2022.04.28 |
| [C] 시간복잡도가 O(n)인 재귀함수로 피보나치 수열 구하기 (0) | 2022.01.23 |
